Understanding Trigonometric Ratios: A Comprehensive Guide:

Introduction:

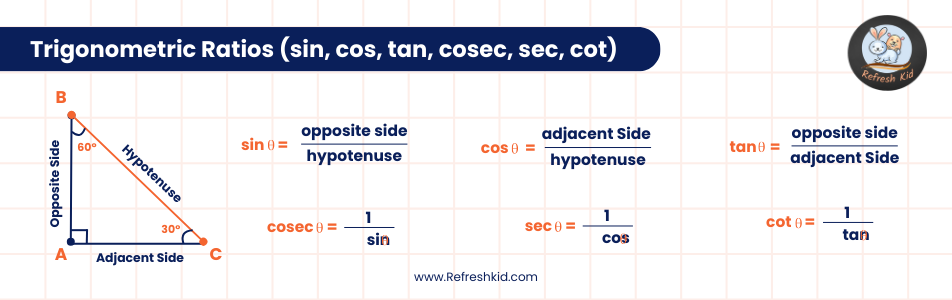
Trigonometry, an essential branch of mathematics, delves into the relationships between the angles and sides of triangles. Central to this field are trigonometric ratios, fundamental tools that offer a deep understanding of geometric properties. In this comprehensive guide, we'll explore the six primary trigonometric ratios—sine, cosine, tangent, cotangent, secant, and cosecant—providing you with the knowledge to tackle a wide array of mathematical and real-world problems.

The Essence of Trigonometric Ratios:

Trigonometric ratios are a cornerstone of mathematics, particularly in fields like engineering, physics, and architecture. These ratios define the relationship between the angles and sides of right-angled triangles, paving the way for solving complex problems with ease. Let's dive into the basics:

Sine (sin): The ratio of the length of the opposite side to the hypotenuse $=\frac{height}{hypotenuse}$ . Picture yourself standing on a beach, the sine ratio is like the height of the wave compared to its full potential.
Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse. $=\frac{base}{hypotenuse}$ . Think of cosine as the shadow cast by a lighthouse beam on the shore, linking the adjacent side with the hypotenuse.
Tangent (tan): The ratio of the length of the opposite side to the adjacent side $=\frac{height}{base}$ . Envision a tall tree, with tangent representing the tree's shadow length compared to its height from your viewpoint.

Expanding beyond these, we also have the reciprocal trigonometric ratios:

Cotangent (cot): The reciprocal of tangent, i.e., adjacent/opposite.
Secant (sec): The reciprocal of cosine, i.e., hypotenuse/adjacent.
Cosecant (csc): The reciprocal of sine, i.e., hypotenuse/opposite.

Applications and Importance:

Understanding trigonometric ratios opens doors to numerous applications in various fields. From designing architectural marvels and bridges to navigating the vast oceans and understanding the orbits of celestial bodies, these ratios are invaluable. They are also crucial in the analysis of waves, from sound waves in acoustics to light waves in optics.

Practical Examples and Problem-Solving:

To harness the power of trigonometric ratios, one must be adept at applying them to practical scenarios. Consider a scenario where you need to calculate the height of a mountain or a building; trigonometric ratios can provide a precise answer without the need for physical measurement. This application, known as triangulation, is a testament to the versatility and utility of trigonometry.

Learning and Mastery:

Mastering trigonometric ratios requires practice and a solid understanding of their geometric interpretations. Visualizing these ratios as part of a right-angled triangle can significantly aid in grasping their concepts. Engaging with interactive tools, educational videos, and practice problems can enhance your learning experience, allowing you to apply trigonometric ratios confidently in various situations.

Conclusion:

Trigonometric ratios are more than just mathematical expressions; they are the bridge connecting abstract mathematics with the tangible world around us. Whether you're a student embarking on your mathematical journey, a professional seeking to refine your skills, or simply a curious mind intrigued by the beauty of mathematics, understanding trigonometric ratios is a step toward unlocking a world of possibilities. Embrace the challenge, and let trigonometry illuminate your understanding of the world.