Volume of cubes and cuboids

Mastering Volume Calculations for Cubes and Cuboids:

Introduction:

Understanding how to calculate the volume of basic geometric shapes like cubes and cuboids is a fundamental skill in mathematics. Whether you're a student tackling geometry for the first time, a teacher seeking educational content, or simply curious about spatial mathematics, mastering these volume calculations can significantly enhance your mathematical skills. This blog explores the volume formulas for cubes and cuboids and provides practical numerical examples to solidify your understanding.

What are Cubes and Cuboids?

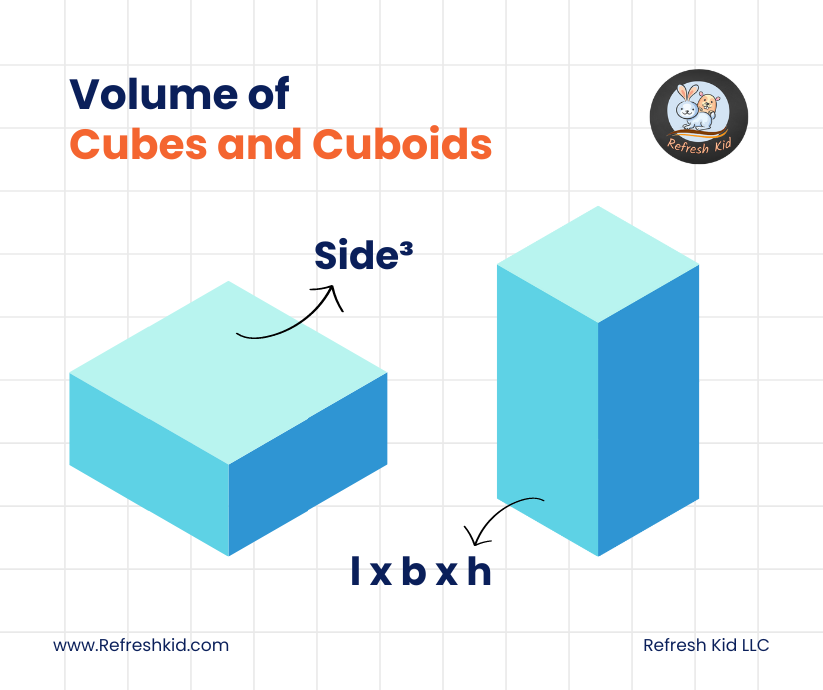
A cube is a three-dimensional shape with six equal square faces, each meeting the other at 90 degrees. A key characteristic of a cube is that all its edges (length, width, and height) are equal.

A cuboid, also known as a rectangular prism, resembles a cube but with varying lengths for its edges. A cuboid has six rectangular faces and angles of 90 degrees between adjacent faces.

Volume Formulas:

Calculating the volume of these shapes involves straightforward formulas that apply the basic principles of area calculation extended into three dimensions. 

Cube Volume Formula:

The volume of a cube can be calculated using the formula:

Where:
  is the length of any side of the cube.

Cuboid Volume Formula:

The volume of a cuboid is given by:

Where:
- is the length,
- is the width,
- is the height of the cuboid.

Numerical Examples:

Example 1: Volume of a Cube

Let's calculate the volume of a cube with each side measuring 4 cm.

Using the formula:

Thus, the volume of the cube is 64 cubic centimeters.

Example 2: Volume of a Cuboid

Consider a cuboid with a length of 8 cm, a width of 3 cm, and a height of 2 cm.

Applying the volume formula:

The volume of this cuboid is 48 cubic centimeters.

Calculating Volume for Practical Applications:

Example 3: 

Imagine you need to fill a water tank that is shaped like a cuboid, measuring 2 meters in length, 1.5 meters in width, and 1 meter in height.

This tank can hold up to 3 cubic meters of water.

Example 4: 

Imagine a classroom that needs to be measured for air conditioning requirements. The classroom dimensions are 20 meters in length, 10 meters in width, and 3 meters in height.

Using the volume formula for a cuboid:

Where m, m, and m:

The volume of the classroom is 600 cubic meters, which is crucial information for determining the appropriate air conditioning capacity.

Example 5: 

A decorative cube is used as a centerpiece in a gallery, with each side measuring 0.5 meters.

The volume of the decorative cube is 0.125 cubic meters, indicating its compact size that contributes aesthetically without overwhelming the space.

These examples provide a practical approach to understanding volume calculations for cubes and cuboids in various contexts, enhancing the blog's utility and relatability for readers looking to apply these mathematical concepts in everyday scenarios.

Conclusion

The ability to calculate the volume of cubes and cuboids is invaluable not only in academic settings but also in real-life applications, such as in construction, manufacturing, and day-to-day problem-solving. By understanding these formulas and practicing with examples, students and professionals can improve their spatial awareness and mathematical reasoning. Keep exploring our website for more resources and tutorials to further your expertise in geometry and other mathematical areas!

These calculations, while simple, play a crucial role in various fields, helping to solve practical problems efficiently and effectively. Whether for educational purposes, professional projects, or personal curiosity, mastering volume calculations is an essential skill in geometry.