Special Right Triangles

Mastering Special Right Triangles: The Key to Simplifying Geometry:

Introduction:

Dive into the fascinating realm of special right triangles, an essential cornerstone of geometry that streamlines mathematical calculations and deepens our understanding of geometric principles. This detailed guide sheds light on the intriguing characteristics and practical applications of 30-60-90 and 45-45-90 triangles, offering valuable insights for students, educators, and math enthusiasts alike. Embark on a journey to unravel the mysteries of these geometric marvels and harness their potential to solve complex problems with ease.

Exploring the Fundamentals of Special Right Triangles:

Special right triangles stand out in geometry due to their unique angle measurements and side length ratios, which provide a reliable foundation for solving a wide array of mathematical problems. The two most notable types are the 30-60-90 triangle and the 45-45-90 triangle, each distinguished by its specific properties and applications.

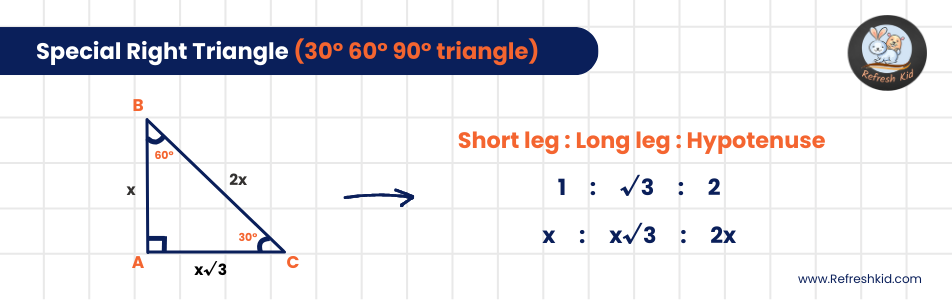
Delving into the 30-60-90 Triangle:

The 30-60-90 triangle features angle measurements of 30 degrees, 60 degrees, and 90 degrees, creating a perfect harmony that results in side lengths following a 1:√3:2 ratio. This proportion relates the shortest side, the side opposite the 60-degree angle, and the hypotenuse, respectively, offering a simplified approach to tackling geometry tasks involving this type of triangle.

Understanding the 45-45-90 Triangle:

Also known as the isosceles right triangle, the 45-45-90 triangle boasts two 45-degree angles and a 90-degree angle, leading to side lengths that adhere to a 1:1:√2 ratio. This indicates that the legs are of equal length, and the hypotenuse is √2 times longer than a leg, providing a straightforward method for calculating dimensions and angles in geometry and trigonometry.

Practical Applications of Special Right Triangles:

Beyond their theoretical importance, special right triangles have real-world applications in architecture, engineering, design, and daily problem-solving. Their predictable side ratios enable precise calculations, aiding professionals in fields requiring geometric accuracy and efficiency. Additionally, mastering these triangles fosters problem-solving skills and lays a solid foundation for advancing in mathematical studies.

Enhancing Your Understanding of Special Right Triangles:

To fully leverage the benefits of special right triangles in geometry, consider these strategies:

1. Commit the side ratios to memory: Knowing the  ratio for 30-60-90 triangles and the ratio for 45-45-90 triangles can significantly expedite problem-solving processes.
2. Engage with real-world problems: Applying the principles of special right triangles to practical scenarios, such as calculating heights, distances, and angles, reinforces understanding and retention.
3. Use visual aids: Incorporating diagrams, models, and visual representations can clarify the properties and relationships within these triangles, making them more accessible and memorable.

Conclusion:

Special right triangles are more than just a geometric curiosity; they are powerful tools that simplify complex problems and enrich our comprehension of mathematical concepts. By exploring the unique attributes and practical uses of 30-60-90 and 45-45-90 triangles, learners can unlock new dimensions of mathematical proficiency and apply these principles to both academic endeavors and everyday challenges. Delve into the elegance and utility of special right triangles, and let them illuminate your path to geometric mastery and beyond.