Surface area of Cylinders (Lateral and Total Surface Area)

Unlock the Mysteries of Cylinders: Calculating Lateral and Total Surface Area with Practical Examples:

When it comes to understanding the geometry of cylinders, two key concepts often come into play: lateral surface area and total surface area. These measurements are crucial not only in academic contexts but also in real-world applications like engineering, architecture, and manufacturing. In this comprehensive guide, we'll explore the formulas for calculating both lateral and total surface areas of cylinders, accompanied by step-by-step examples to enhance your learning experience.

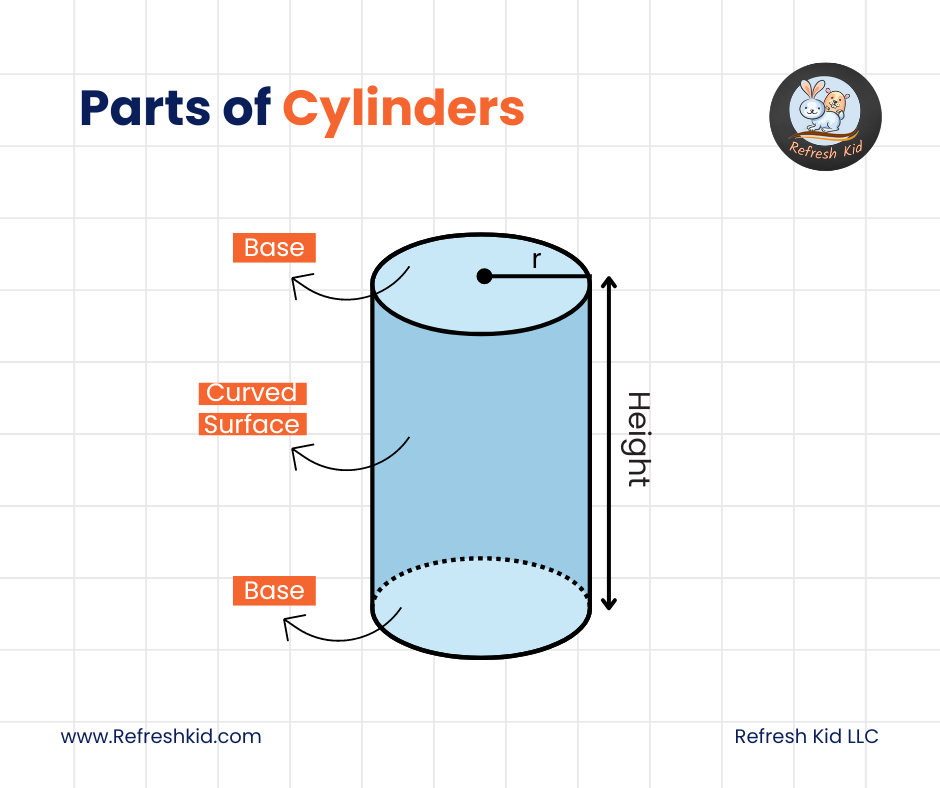
What is a Cylinder?

A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. It can be seen in various objects around us, from a simple soda can to oil drums, or even pillars supporting a structure.

Lateral Surface Area of a Cylinder:

The lateral surface area of a cylinder refers to the area of the curved surface running between the two circular bases. It is crucial for tasks such as painting the outside of a cylindrical tank or wrapping a label around a can.

Formula for Lateral Surface Area:

The formula to calculate the lateral surface area ​ of a cylinder is:

where:

• is approximately 3.14159,
• is the radius of the cylinder's base,
• is the height of the cylinder.

Example Calculation:

Let's calculate the lateral surface area of a cylinder that has a radius of 3 cm and a height of 5 cm.

Total Surface Area of a Cylinder:

The total surface area of a cylinder includes the lateral surface area plus the area of the two circular bases.

Formula for Total Surface Area:

The formula for calculating the total surface area ​ of a cylinder is:

This formula can be broken down into:

• : the lateral surface area,
• : the area of the two bases.

Example Calculation:

Using the same cylinder with a radius of 3 cm and a height of 5 cm, we can find the total surface area:

Mathemical Examples:

Example 1:

Imagine a cylindrical roller with a radius of 0.5 meters and a height of 2 meters. Calculate its lateral surface area:

This calculation is crucial when needing to know how much material is required to cover the roller's surface.

Example 2:

Using the dimensions from Example 1 (cylindrical roller with a radius of 0.5 meters and height of 2 meters), the total surface area is:

This total area is essential for calculating the amount of paint needed to cover the entire roller.

Example 3:

Consider a cylindrical canister used for storing oats, with a radius of 7 cm and a height of 12 cm. Calculate its total surface area:

This measurement helps in designing labels or artwork that would wrap around or cover the canister.

Practical Applications:

Understanding the surface area of cylinders is essential for numerous practical applications. For example, calculating the paint required to cover a water storage cylinder, or determining the material needed for a cylindrical packaging tube.

Conclusion:

Whether you're a student tackling geometry homework, a DIY enthusiast planning a project, or a professional in need of precise calculations for cylindrical objects, understanding how to calculate both lateral and total surface areas is invaluable. By mastering these formulas, you'll enhance your mathematical skills and improve your ability to handle various practical tasks involving cylinders.