Unveiling the Mysteries of Pythagorean Triplets: A Mathematical Exploration

Introduction:

In the realm of mathematics, few concepts spark as much curiosity and intrigue as Pythagorean Triplets. This fascinating topic not only captivates the minds of math enthusiasts but also plays a pivotal role in various applications, from architectural design to computer science. In this blog, we'll embark on a journey to explore the depths of Pythagorean Triplets, unraveling their secrets and understanding their significance in the mathematical world.

What are Pythagorean Triplets?

At the heart of Pythagorean Triplets lies the Pythagorean theorem, a fundamental principle in geometry attributed to the ancient Greek mathematician Pythagoras. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Pythagorean Triplets are sets of three positive integers $(a, b, c)$ that satisfy this equation: $a^2+b^2=c^2$ .

The Magic of Classic Examples:

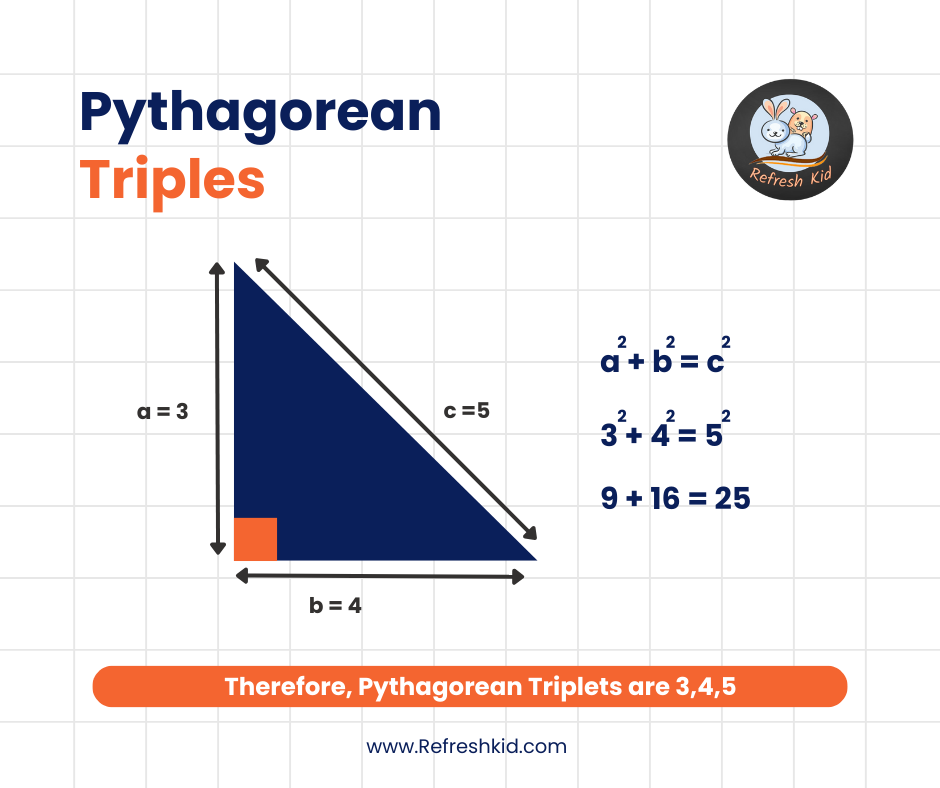
The most well-known example of a Pythagorean Triplet is the set (3, 4, 5). This classic triplet beautifully illustrates the theorem, as $3^2+4^2=9+16=25=5^2$ . Other popular examples include (6, 8, 10), (5, 12, 13), and (7, 24, 25), each demonstrating the theorem's validity and the existence of these unique number sets.

Generating Pythagorean Triplets:

One of the most intriguing aspects of Pythagorean Triplets is their generation. Mathematicians have developed various methods to generate these triplets, one of which involves using two positive integers, m and n, where $m>n$ . By applying the formulas $a=m^2-n^2, b=2mn$ , and $c=m^2+n^2$ , one can generate an infinite number of triplets, showcasing the endless possibilities within this mathematical concept.

Applications Beyond Mathematics:

The applications of Pythagorean Triplets extend far beyond the realm of pure mathematics. In architecture and construction, these triplets offer a reliable method for creating right angles, a cornerstone in building design. In computer science, they play a role in algorithms and data analysis, offering efficient solutions to complex problems. The reach of Pythagorean Triplets even extends into the world of music, where they contribute to the theory behind musical scales and harmonics.

Basic Example of a Pythagorean Triplet:

Start with the most well-known Pythagorean Triplet to lay the foundation:

"The classic Pythagorean Triplet that most people are familiar with is (3, 4, 5). This set satisfies the Pythagorean theorem, where $3^2+4^2=5^2 ( \text{or } 9+16=25)$ , proving that these three numbers form a right-angled triangle."

Generating Pythagorean Triplets:

Introduce a method to generate Pythagorean Triplets using two positive integers, $m$ and $n$ (with $m>n$ ):

"To generate a Pythagorean Triplet, you can use two integers $m$ and $n$ , where $m$ is greater than $n$ . The formulas $a=m^2-n^2, b=2mn$ , and $c=m^2+n^2$ will produce a triplet. For example, if $m=3$ and $n=2$ , we can calculate a triplet as follows: