Law of Cosines

Mar 30 , 2024
By Refreshkid LLC

Unraveling the Mysteries of the Law of Cosines: A Comprehensive Guide:

Introduction:

In the realm of mathematics, certain principles stand as pillars, offering insights and solutions to a multitude of problems. Among these is the Law of Cosines, a powerful tool in trigonometry that enables us to solve triangles, particularly non-right triangles, with ease and precision. This article delves into the depths of this fundamental law, exploring its origins, applications, and significance in various fields.

Understanding the Law of Cosines:

The Law of Cosines, also known as the Cosine Rule, establishes a relationship between the lengths of the sides and the angles of a triangle. Unlike the Pythagorean theorem, which exclusively applies to right triangles, the Law of Cosines extends its reach to all types of triangles, making it an indispensable tool in trigonometry.

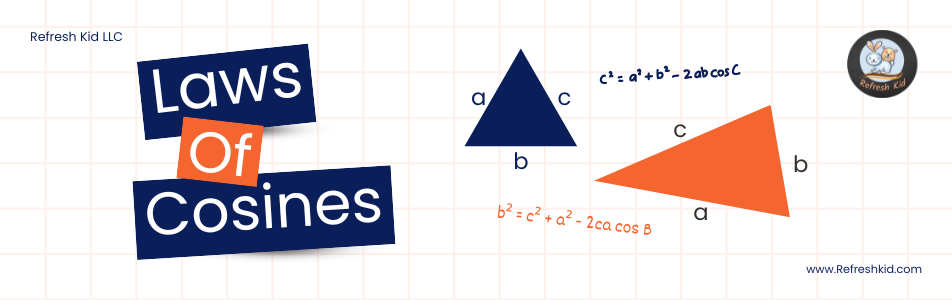
The Law of Cosines states:

$c^2 = a^2 + b^2 - 2ab \cdot \cos(C)$ Where:
- $a\), $b$, and \(c$ represent the lengths of the sides of the triangle.
- $C$ denotes the angle opposite side $c$ .

This formula allows us to compute the length of any side of a triangle if we know the lengths of the other two sides and the angle between them, or to find an angle if we know all three side lengths.

Example 1:

Suppose we have a triangle with side lengths $$ a = 5 $, $ b = 7 $,$ and an angle $C \) between $ a $ and \( b$ measuring $60^\circ$ . We want to find the length of the third side $c$ .

Using the Law of Cosines formula:

$c^2 = a^2 + b^2 - 2ab \cdot \cos(C)$

Substituting the given values:

$c^2 = 5^2 + 7^2 - 2(5)(7) \cdot \cos(60^\circ)$

$c^2 = 25 + 49 - 70 \cdot \frac{1}{2}$

$c^2 = 25 + 49 - 35$

$c^2 = 39$

$c = \sqrt{39} \approx 6.24$

So, the length of the third side $$ c $ is approximately $ 6.24 $.$

Example 2:

Let's consider another triangle with side lengths $a = 8 \), $ b = 10 $, and an angle $ C$ between $a$ and $b$ measuring $\( 45^\circ $.$ We want to find the length of the third side $c$ .

Using the Law of Cosines formula:

$c^2 = a^2 + b^2 - 2ab \cdot \cos(C)$

Substituting the given values:

$c^2 = 8^2 + 10^2 - 2(8)(10) \cdot \cos(45^\circ)$

$c^2 = 64 + 100 - 160 \cdot \frac{\sqrt{2}}{2}$

$c^2 = 164 - 80\sqrt{2}$

$c \approx \sqrt{164 - 80\sqrt{2}}$

$c \approx 4.47$

So, the length of the third side $c$ is approximately $4.47$ .

These examples illustrate how to use the Law of Cosines to find the length of a side of a triangle when you have the lengths of the other two sides and the angle between them.

Applications of the Law of Cosines:

1. Navigation and Surveying: In navigation and surveying, accurate measurements are crucial for charting courses and determining distances. The Law of Cosines facilitates the calculation of distances between points on a map or the position of an object based on observed angles and distances.

2. Physics and Engineering: The Law of Cosines finds extensive application in physics and engineering, particularly in problems involving forces, velocities, and distances. It helps analyze the trajectories of projectiles, the tensions in structures, and the forces acting on objects at angles.

3. Astronomy: Celestial navigation relies on precise calculations to determine the positions of stars, planets, and other celestial bodies. The Law of Cosines aids astronomers in measuring distances between heavenly bodies and predicting their movements.

4. Computational Geometry: In computer graphics and computational geometry, algorithms often require solving geometric problems efficiently. The Law of Cosines serves as a fundamental tool for solving such problems, enabling the creation of realistic 3D models and simulations.

Derivation and Proof:

The Law of Cosines can be derived from the Law of Sines or by considering the Law of Cosines for acute triangles and then extending it to all triangles using the concept of the supplement of an angle. Its proof involves applying the Pythagorean theorem to the triangle formed by dropping a perpendicular from one vertex to the opposite side.

Let's consider a triangle ABC, where side $c$ is opposite angle $C$ . Dropping a perpendicular from vertex $B$ to side $AC$ divides the triangle into two right triangles. Applying the Pythagorean theorem to one of these right triangles yields:

$b^2 = h^2 + x^2$

Where:
- $h$ represents the length of the perpendicular segment.
- $x$ denotes the length of the segment of side $a$ .

Similarly, for the other right triangle, we have:

$a^2 = h^2 + (c - x)^2$

Expanding and simplifying these equations lead to the Law of Cosines.

Conclusion:

The Law of Cosines stands as a testament to the elegance and universality of mathematical principles. Its versatility and applicability extend across various domains, from navigation and physics to astronomy and computer science. By understanding and harnessing the power of this fundamental law, mathematicians, scientists, and engineers continue to unravel the mysteries of the universe and forge new paths in exploration and discovery.