Inscribed Angles, Intercepted Arc, Inscribed Angles Theorem

Exploring Inscribed Angles, Intercepted Arcs and the Inscribed Angles Theorem:

Introduction:

Inscribed angles and intercepted arcs are fundamental concepts in geometry, particularly when dealing with circles. Understanding these concepts not only helps in solving problems related to circle geometry but also lays the groundwork for more advanced mathematical concepts. In this blog post, we'll dive into inscribed angles, explore the relationship between inscribed angles and intercepted arcs, and discuss the Inscribed Angles Theorem.

I. Inscribed Angles:

An inscribed angle is formed when two chords of a circle intersect at a point on the circle's circumference. The vertex of the angle lies on the circle itself. The key property of an inscribed angle is that its measure is half the measure of its intercepted arc. This relationship is crucial in solving various circle geometry problems.

II. Intercepted Arc:

The intercepted arc of an inscribed angle is the arc lying between the angle's sides. In other words, it is the portion of the circle's circumference that lies inside the inscribed angle. The measure of the intercepted arc is directly related to the measure of the inscribed angle, as stated earlier.

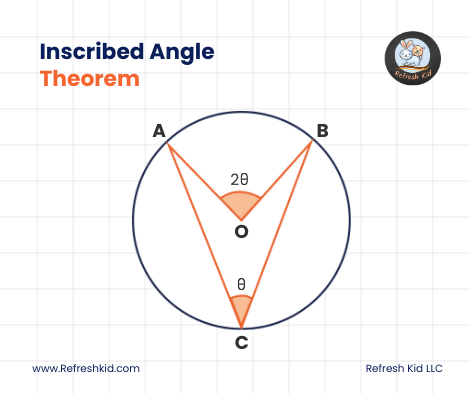
III. Inscribed Angles Theorem:

The Inscribed Angles Theorem, also known as the Inscribed Angle Theorem or the Central Angle Theorem, states that an inscribed angle in a circle is half the measure of its intercepted arc. Mathematically, it can be expressed as follows:

This theorem forms the basis for many circle geometry proofs and is often used to establish relationships between angles and arcs within circles.

IV. Examples and Applications:

Let's delve into numerical examples involving inscribed angles, intercepted arcs, and the Inscribed Angles Theorem.

Example 1:

In a circle with center O, let's say the measure of arc AB is 120 degrees. An inscribed angle AOB intercepts this arc. What is the measure of angle AOB?

Solution:

According to the Inscribed Angles Theorem, the measure of an inscribed angle is half the measure of its intercepted arc.
So, angle AOB =  .

Example 2:

In a circle with center O, the measure of arc XY is 150 degrees. If angle XYZ is an inscribed angle, what is the measure of angle XYZ?

Solution:

Using the Inscribed Angles Theorem, we know that the measure of an inscribed angle is half the measure of its intercepted arc.
So, angle XYZ = .

Example 3:

In a circle with center O, arc CD measures 90 degrees. If angle CED is an inscribed angle, what is the measure of angle CED?

Solution:

Again, applying the Inscribed Angles Theorem, we find that angle CED =

Example 4:

In a circle with center O, if angle DEF measures 80 degrees, what is the measure of the intercepted arc DF?

Solution: 

Given that angle DEF = 80 degrees, by the Inscribed Angles Theorem, the intercepted arc DF will be twice that measure, so arc DF = 2 * 80 degrees = 160 degrees.

Example 5:

In a circle with center O, if arc GH measures 120 degrees, and angle GIO is an inscribed angle, what is the measure of angle GIO?

Solution:

Using the Inscribed Angles Theorem, angle GIO =

These examples illustrate the application of the Inscribed Angles Theorem in finding the measures of angles and intercepted arcs in a circle.

Conclusion:

Inscribed angles, intercepted arcs, and the Inscribed Angles Theorem are essential concepts in circle geometry, offering insights into the relationship between angles and arcs within circles. Mastery of these concepts not only strengthens one's understanding of geometry but also lays the foundation for more advanced mathematical concepts. Whether you're a student learning geometry or a math enthusiast exploring the intricacies of circle geometry, understanding inscribed angles and their properties is a valuable asset.