Concentric, Coplanar, and Congruent Circles

Understanding the Geometry of Circles: Concentric, Coplanar, and Congruent Circles

Introduction:

Circles, one of the most fundamental shapes in geometry, possess unique properties and relationships that have fascinated mathematicians for centuries. Among the various classifications, concentric circles, coplanar circles, and congruent circles stand out as important concepts in understanding the intricacies of circle geometry. In this blog, we delve into each of these types of circles, exploring their definitions, properties, and applications.

Concentric Circles:

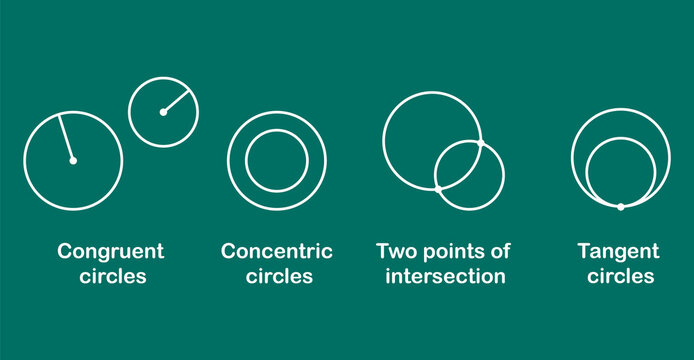
Concentric circles are circles that share the same center but have different radii. Visually, they resemble a series of circles nested within one another, like the rings of a tree. The term "concentric" originates from the Latin words "con," meaning together, and "centrum," meaning center.

Properties:

1. Common Center: All concentric circles share a common center point.
2. Different Radii: Each concentric circle has a different radius length while maintaining the same center.
3. Equidistant Points: Any two points on concentric circles that are equidistant from the center will have the same difference in distance.

Applications:

Concentric circles find applications in various fields, including engineering, architecture, and design. In engineering, they are utilized in gear systems, bearings, and pulleys, where different components rotate around a common axis.

Coplanar Circles:

Coplanar circles are circles that lie in the same plane. The term "coplanar" refers to objects or points that exist within the same two-dimensional plane.

Properties:

1. Shared Plane: Coplanar circles share the same flat surface or plane.
2. No Intersection: While coplanar circles may share the same plane, they do not necessarily intersect or touch each other.

Applications:

In geometry and trigonometry, coplanar circles are fundamental for understanding concepts such as tangent lines, secants, and chord properties. They are also relevant in graphic design and architecture for creating patterns, layouts, and geometric shapes.

Congruent Circles:

Congruent circles are circles that have the same size and shape. In other words, their radii are equal, and their corresponding points are equidistant from the center.

Properties:

1. Equal Radii: Congruent circles have radii of equal length.
2. Same Shape and Size: They share identical shapes and sizes, with every point on one circle having a corresponding point at the same distance from the center on the other circle.

Applications:

Congruent circles play a crucial role in geometry, especially in the study of similarity and transformations. They are used in various geometric constructions, such as creating tangent circles or constructing polygons with specific properties.

Conclusion:

Concentric circles, coplanar circles, and congruent circles are essential concepts in geometry with distinct properties and applications. Understanding these types of circles not only enriches our knowledge of geometry but also enhances our ability to analyze and solve real-world problems across diverse fields. Whether in engineering, architecture, or mathematics, circles continue to inspire curiosity and exploration, revealing the beauty and complexity of mathematical relationships in the world around us.