Circles and Tangents

Exploring Circles and Tangents: A Journey into Geometric Beauty:

Circles, with their perfect symmetry and infinite points equidistant from the center, have intrigued mathematicians and thinkers for centuries. In the realm of geometry, one of the most fascinating aspects of circles is their interaction with tangents. Tangents, those lines that touch a circle at exactly one point, create a rich tapestry of relationships and properties when they intersect with circles. In this blog, we will embark on a journey to unravel the mysteries of circles and tangents, exploring their significance and applications through numerical examples.

Understanding Tangents:

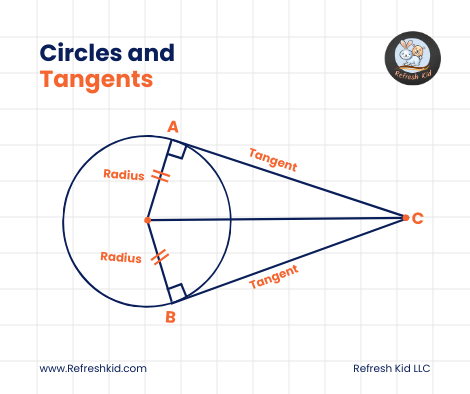
Before delving into the intricacies of tangents and circles, let's ensure we grasp the concept of tangency. A tangent is a line that intersects a circle at exactly one point, known as the point of tangency. This means that at the point of tangency, the tangent is perpendicular to the radius drawn to that point.

Properties of Tangents:

1. Perpendicularity: At the point of tangency, the tangent is perpendicular to the radius of the circle.
2. Length Equality: Tangents drawn from an external point to a circle are equal in length.
3. Angle Relationships: Various angle relationships exist between tangents, secants, and chords intersecting a circle.

Numerical Examples:

Example 1:

Consider a circle with radius 5 units. A tangent is drawn to this circle from a point external to it, at a distance of 8 units from the circle's center. What is the length of the tangent?

Solution:

Given that the distance from the external point to the circle's center is 8 units, and the radius is 5 units, we can apply the Pythagorean theorem to find the length of the tangent.

Using Pythagoras:

So, the length of the tangent is approximately 6.24 units.

Example 2:

In a circle with radius 6 cm, a tangent is drawn from an external point at a distance of 10 cm from the circle's center. Find the length of the tangent.

Solution:

Using the same formula as before:

Thus, the length of the tangent is 8 cm.

Here are some more numerical examples on finding the length of a tangent:

Example 3: 

   - Radius of the circle (r) = 5 units
   - Distance from the center to the point of tangency (d) = 12 units

Find the length of the tangent .

Solution:

   - Using the Pythagorean theorem, the length of the tangent (l) can be calculated as:
   
   - Substituting the values, units.

Example 4:

   - Radius of the circle (r) = 3.5 units
   - Distance from the center to the point of tangency (d) = 8 units

Find the length of the tangent.

Solution:

   - Using the Pythagorean theorem, the length of the tangent (l) can be calculated as:
   
   - Substituting the values, units.

Example 5: 

   - Radius of the circle (r) = 10 units
   - Distance from the center to the point of tangency (d) = 15 units

Find the length of the tangent.

Solution:

   - Using the Pythagorean theorem, the length of the tangent (l) can be calculated as:
     
   - Substituting the values,  units.

Applications of Circles and Tangents:

1. Optics: In optics, tangents play a crucial role in understanding the reflection and refraction of light rays at curved surfaces, such as lenses and mirrors.
2. Engineering: Tangents are employed in engineering disciplines for designing curves, roads, railways, and other structures that require smooth transitions.
3. Navigation: In navigation and cartography, tangents help in determining the trajectory of movement and estimating distances.

In conclusion, circles and tangents form a fundamental aspect of geometry with diverse applications across various fields. Through numerical examples and exploration of their properties, we gain a deeper understanding of their significance in mathematics and beyond. So, the next time you encounter a circle, remember the profound interplay it shares with tangents, and appreciate the elegance of their relationship.