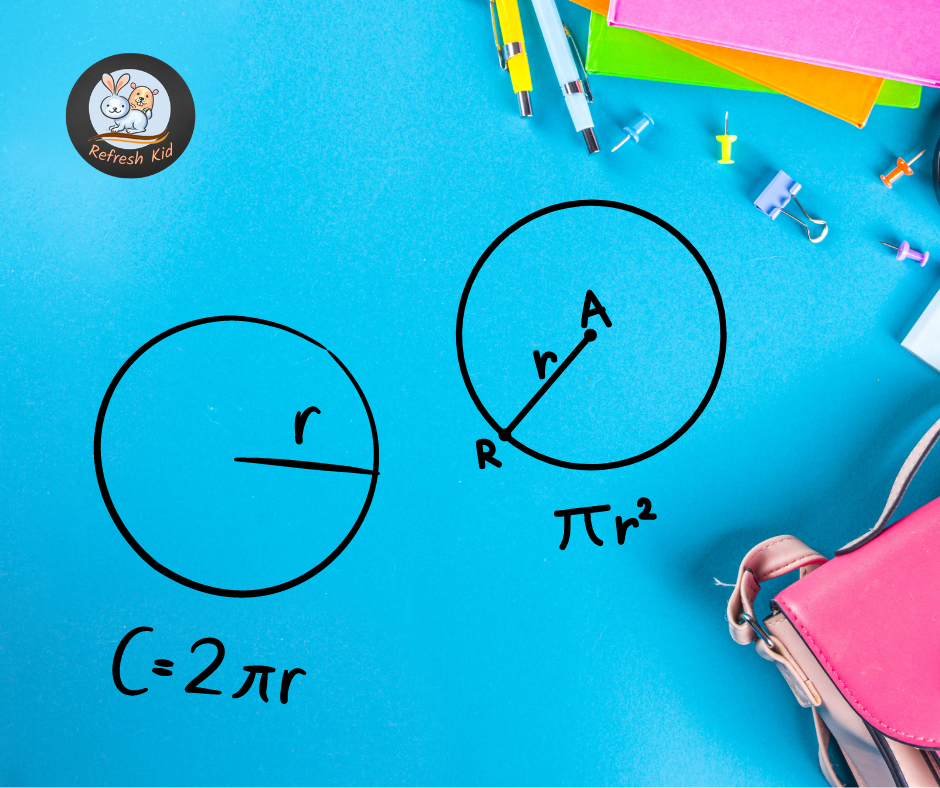Area and Circumference of a Circle

Apr 04 , 2024
By Refreshkid LLC

Unraveling the Mysteries of Circles: Understanding Area and Circumference:

Circles are one of the most fundamental shapes in geometry, possessing unique properties that have intrigued mathematicians and thinkers for centuries. Among the many properties of circles, two stand out as particularly important: the area enclosed by a circle and the distance around its outer edge, known as the circumference. In this blog post, we'll delve into the formulas for calculating these values and explore their significance.

Understanding the Basics:

Before we dive into the formulas, let's revisit some basic concepts:

1. Radius (r):

The distance from the center of the circle to any point on its edge. It is denoted by $r$ .

2. Diameter (d):

The distance across the circle through its center, which is twice the radius. It is denoted by $d$ .

3. P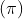i $( \pi \)$ :

A mathematical constant representing the ratio of the circumference of a circle to its diameter. Its approximate value is $3.14159$ , although it is an irrational number with infinite decimal places.

Calculating Circumference:

The circumference of a circle is the total length of its boundary. It is given by the formula:

$C = 2\pi r$

Where:
- $C$ is the circumference.
- $\pi$ is the mathematical constant, approximately equal to $3.14159$ .
- \ $( r \)$ is the radius of the circle.

This formula tells us that to find the circumference, we simply multiply the radius by $2\pi$ .

Calculating Area:

The area of a circle is the total space enclosed by its boundary. It is given by the formula:

$A = \pi r^2$

Where:
- $A$ is the area.
- $\pi$ is the mathematical constant, approximately equal to $3.14159$ .
- $r$ is the radius of the circle.

This formula tells us that to find the area, we square the radius and multiply it by $\pi$ .

Here are examples of how to find the area and circumference of a circle:

Example 1:

Let's say we have a circle with a radius of 5 units.

-To find the circumference:
Circumference = $2\times \pi \times radius$
Circumference = $2\times \pi \times 5$ = $10\pi \$ units

- To find the area:
Area = $\pi \times radius\wedge 2$
Area = $\pi \times 5\wedge 2$ = $25\pi \$ square units

Example 2:

Suppose we have a circle with a diameter of 10 cm.

- To find the circumference:
Circumference = $\pi \times diameter$
Circumference = $\pi \times 10$ = $10\pi \$ cm

- To find the area:
Area = $\pi \times (diameter/2)^2$
Area = $\pi \times (10/2)^2$ = $25\pi \$ square cm

Example 3:

Consider a circle with a radius of 3.5 meters.

- To find the circumference:
Circumference = $2 \times \pi \times radius$
Circumference = $2 \times \pi \times 3.5 = 7\pi$ meters

- To find the area:
Area = $\pi \times radius^2$
Area = $\pi \times 3.5^2$ = $12.25\pi \$ square meters

These examples demonstrate how to calculate the circumference and area of a circle given either the radius or diameter. Remember, π (pi) is a mathematical constant approximately equal to 3.14159, which is often rounded to 3.14 for practical calculations.

Significance and Applications:

Understanding the area and circumference of circles has myriad real-world applications:

1. Engineering and Construction: Engineers and architects use these formulas when designing structures with circular components, such as bridges, arches, and wheels.

2. Physics: Circles frequently appear in physics equations, particularly in the study of motion and forces. Understanding their properties is crucial in fields like mechanics and astronomy.

3. Technology: Circles are prevalent in technology, from the design of computer graphics to the mechanics of gears and pulleys.

4. Art and Design: Artists and designers often incorporate circular shapes into their creations. Understanding the mathematical properties of circles can inform their aesthetic choices and compositions.

Conclusion:

Circles are not just abstract mathematical concepts; they are pervasive in our everyday lives and essential to understanding the world around us. Whether you're marveling at the perfect symmetry of a wheel or calculating the dimensions of a circular structure, the formulas for the area and circumference of circles provide invaluable tools for exploration and discovery. So the next time you encounter a circle, remember the beauty and significance encapsulated within its simple yet elegant geometry.