Understanding Angles and Arcs in Circles: A Comprehensive Guide:

Introduction:

Circles are among the most fundamental geometric shapes, and they play a significant role in various fields such as mathematics, engineering, and design. One of the key elements of a circle is its angles and arcs, which are essential for understanding properties like circumference, area, and sector divisions. In this blog post, we'll delve into the world of angles and arcs within circles, exploring their definitions, properties, and applications.

Angles in a Circle:

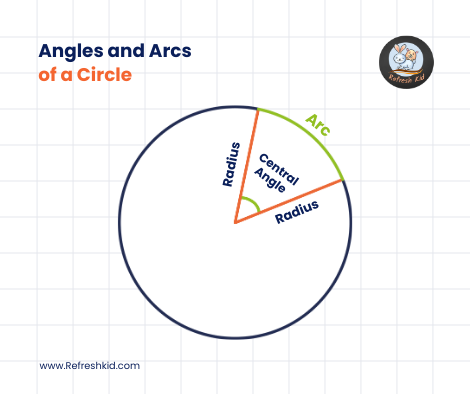
In a circle, an angle is formed when two rays originate from the same point, called the vertex, and extend to intersect the circle at two distinct points. The angle is measured by the amount of rotation required to superimpose one ray onto the other, starting from the initial position.

Central Angle: A central angle is an angle whose vertex is the center of the circle. It subtends an arc on the circumference of the circle. The measure of a central angle is equal to the measure of its intercepted arc.

Inscribed Angle: An inscribed angle is an angle formed by two chords in a circle, with the vertex lying on the circumference. The measure of an inscribed angle is half the measure of its intercepted arc.

Properties of Angles:

1. The sum of the central angles in a circle is always 360 degrees.
2. Angles inscribed in the same arc are equal.
3. Angles subtended by the same chord are equal.
4. Angles formed by tangents drawn to the circle from an external point are equal.

Arcs in a Circle:

An arc in a circle is a portion of the circumference. It is defined by two points on the circumference and the continuous curve connecting them.

Minor Arc: A minor arc is an arc of a circle that measures less than 180 degrees. It is the shorter of the two arcs determined by endpoints of an inscribed angle.

Major Arc: A major arc is an arc of a circle that measures more than 180 degrees. It is the longer of the two arcs determined by endpoints of an inscribed angle.

Semicircle: A semicircle is an arc of a circle that measures exactly 180 degrees. It is half of the circle's circumference, and its endpoints are diametrically opposite each other.

Properties of Arcs:

1. The measure of a minor arc plus the measure of its corresponding major arc is always 360 degrees.
2. The measure of a semicircle is always 180 degrees.
3. Angles subtended by the same arc are equal.
4. Angles subtended by the diameter are always right angles.

Applications:

Understanding angles and arcs in circles has practical applications in various fields:
Engineering: Calculating angles and arcs is crucial in designing machinery parts like gears and pulleys.
Architecture: Architects use circular shapes and arcs in designing structures like arches and domes.
Navigation: Understanding angles and arcs is essential for navigation, especially in aviation and maritime industries.

Conclusion:

Angles and arcs are fundamental elements of circles, with diverse applications across various fields. Mastering their properties and relationships not only enriches our understanding of geometry but also enhances our problem-solving abilities in real-world scenarios. Whether you're an engineer, architect, or mathematician, a solid grasp of angles and arcs in circles is indispensable. So, let's continue exploring the fascinating world of geometry and its practical implications.